Hello all!

I am officially opening a new project "DB CF ODLS of order 9" .
This is not a BOINC project yet, but a manual project. I have been working on a project for a long time on a PC.
But you can turn a manual project into a BOINC project if you want.

You can find out more here
https://boinc.progger.info/odlk/forum_thread.php?id=165&postid=6222

The second search strategy for 9th order ODLC is Belyshev's program generator_kf_odlk9.
This strategy is described in the topic.
There is nothing to do here at all: I launched the program and forgot.
The program will run until it checks for CF margins in the entire specified rule.
Ready generator CF ODLS!

I post software for this search strategy (Yandex.Disk)
https://yadi.sk/d/8oNQldIm79JJMA

Only one Belyshev program generator_kf_odlk9.exe works in this strategy.
Read the file readme.txt written by the author.

The archive includes sources, these are original author's sources.

Examples of using this strategy are given in the topic
https://boinc.progger.info/odlk/forum_thread.php?id=44
I have worked quite a lot on this strategy.

Let me remind you : there are 20 rules.
You write the rule number from (1 - 20) to the file config.txt .
You may not need to specify the starting SN DLS (In this case delete the start.txt file).
In this case, the program will start searching from the beginning of the specified rule.

Having all the sources, you can easily start a search in a separate Application in any active BOINC project.

Let's see the OEIS sequence
https://oeis.org/A287695

Maximum number of normalized diagonal Latin squares that can be orthogonal to the same diagonal Latin square of order n.

It is written there

a(9) >= 516

I found DLS of order 9 which has 614 ODLS

0 2 5 4 7 3 8 6 1
5 1 6 7 8 2 4 0 3
8 4 2 5 6 0 3 1 7
6 8 0 3 2 7 1 5 4
1 0 3 8 4 6 7 2 5
4 7 1 6 3 5 2 8 0
7 3 8 0 5 1 6 4 2
3 5 4 2 1 8 0 7 6
2 6 7 1 0 4 5 3 8

We now have a(9) >= 614.

The illustration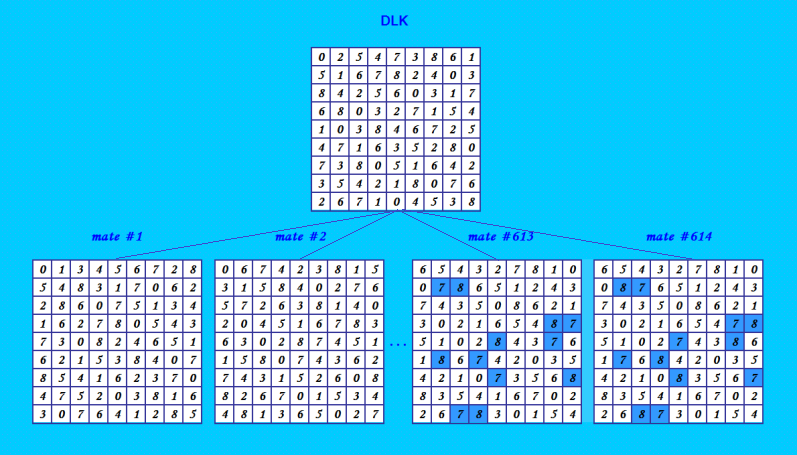



You can improve this result.